jh2song

항상 잘 하고 싶은 사람.

선형대수 2강 선형방정식 강의노트

1 분 소요

선형방정식

$a_1x_1 + a_2x_2 + … + a_nx_n = b$ 와 같은 방정식을

선형방정식(linear equation)이라 한다. 선형방정식은 일차방정식 이라고도 한다.

연립선형방정식

특정 미지수에 대한 선형방정식들이 모여 있는 것을 연립선형방정식 (system of linear equations) 또는 선형시스템 (linear system)이라고 한다.

  • 해집합(solution set)
    • 연립선형방정식의 해를 모아놓은 집합
  • 연립선형방정식의 해가 존재하는 형태
    • 하나의 해를 갖는 경우
    • 해가 존재하지 않는 경우 = 불능, 모순
    • 해가 무수히 많은 경우 = 부정

동치인 연립선형방정식

같은 미지수에 대하여 두 연립선형방정식이 동일한 해집합을 가지면, 두 연립방정식은 동치(equivalent)라고 한다.

  • 동치인 연립선형방정식을 만드는 연산
    • 두 선형방정식의 위치를 교환하는 것
    • 선형방정식의 양변에 0이 아닌 상수를 곱하는 것
    • 특정 선형방정식의 0이 아닌 상수배를 다른 선형방정식에 더하는 것

대입법과 소거법

  • 대입법(elimination method)
    • 특정 미지수를 다른 미지수(들)의 식으로 표현하여, 해당 미지수에 이 식을 대입하여 해를 구하는 방법
    \[\begin{cases} x_1 + 2x_2 = 5 \; ... \; ① \\ 2x_1 + 3x_2 = 8 \; ... \; ② \end{cases} \\ \text{①을 $x_1$에 대한 식으로 바꾸면} \\ x_1 = -2x_2 + 5 \; ... \; ③ \\ \text{②의 $x_1$에 ③의 우변을 대입하면} \\ 2(-2x_2 + 5) + 3x_2 = 8 \; \Rightarrow \; -x_2 + 10 = 8 \; \Rightarrow \; x_2 = 2 \\ \text{$x_2 = 2$를 ③의 $x_2$에 대입하면} \\ x_1 = -2x_2 + 5 = -2(2) + 5 = 1 \\ \text{따라서 해는 $x_1 = 1, x_2 = 2$}\]
  • 소거법
    • 동치인 연립선형방정식을 만드는 연산을 사용해 방정식에서 미지수를 제거하며 해를 구하는 방법
    \[\begin{cases} x_1 + 2x_2 = 5 \; ... \; ① \\ 2x_1 + 3x_2 = 8 \; ... \; ② \end{cases} \\ \text{①에 -2를 곱하면,} \\ \begin{cases} -2x_1 - 4x_2 = -10 \; ... \; ③ \\ 2x_1 + 3x_2 = 8 \; ... \; ② \end{cases} \\ \text{③과 ②를 더하면,} \\ -x_2 = -2 \; \Rightarrow \; x_2 = 2 \\ \text{$x_2 = 2$를 ①에 대입하면} \\ x_1 + 2(2) = 5 \\ \text{그러므로 해는 $x_1 = 1, x2 = 2$}\]

행렬과 연립선형방정식

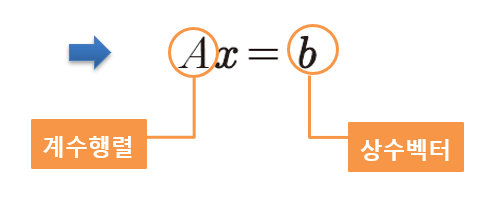
image

  • 행렬방정식
    • 연립선형방정식을 행렬과 벡터의 곱으로 $Ax = b$와 같이 표현한 것을 행렬방정식(matrix equation)이라고 한다.
  • 동치인 연립선형방정식을 만드는 연산과 행렬방정식의 행 연산
    • 두 선형방정식의 위치를 교환하는 것은 행렬방정식의 계수행렬과 상수벡터에서 대응하는 두 행을 교환하는 것과 같다.
    • 선형방정식의 양변에 0이 아닌 상수를 곱하는 것은 행렬방정식의 계수행렬과 상수벡터에서 대응하는 행에 해당 상수를 곱하는 것과 같다.
    • 특정 선형방정식의 0이 아닌 상수배를 다른 선형방정식에 더하는 것은 행렬방정식의 계수행렬과 상수벡터에서 대응하는 한 행의 상수배를 다른 행에 더하는 것과 같다.

나머지는 다음 주차 후에…

참고